Source Cataloguing
The longer you point your telescope at a patch of sky, the fainter the sources you can hope to detect. But no matter how long you stare, the basic challenge remains : distinguishing signal from noise. This can never be done with 100% perfection, there are always errors that creep in that mean you miss a source here, make an inaccurate measurement there, and mistake some noise for a real galaxy over in the back corner. So how exactly do we go about quantifying our mistakes ?
Quantifying quality
There's a big difference between what are data is capable of detecting and what it is we actually do detect when searching it. Even if we point the telescope at a galaxy that's just bursting at the guts with HI, there's no guarantee we'll find it in our data. This leads to two key concepts :
- COMPLETENESS is the fraction of real sources present we manage to detect, at least those which are in principle possible for us to detect.
- RELIABILITY is the fraction of our claimed detections which correspond to real, astrophysical sources.
These terms apply outside the world of astronomy too*. Pay close attention if your guide says, "don't worry, 99% of everything I identify as a tiger turns out to actually be a tiger", as opposed to, "don't worry, I can spot 99% of all tigers present" ! Unfortunately, the media tends to overwhelmingly prefer the usually meaningless term "accuracy", but see below.
* And indeed have implications for non-astronomy space research, such as the prospect of "stealth in space".
Both of these terms depend on the characteristics of both the data (see "Sensitivity" below) and the sources you search for. A "completeness limit" thus means the properties of the sources with which you believe you have detected, say >90% of all such sources. This could be a simple number (e.g. the magnitude of a galaxy) or a more complex set of parameters.
It's surprisingly easy to get either of these numbers to approach 100%... the tricky part is getting both at the same time. For example, if you set your source criteria to include pretty much everything, no matter how faint, you're guaranteed to pick up nearly everything. The problem is that you'll also pick up all the noise as well, so your completeness might be 99% but your reliability only 1%. This can mean searching through a huge catalogue of possible detections of which almost everything is a load of rubbish. At some point, practicality rears its ugly head and you have to make compromises. There's no point having a tonne of gold if it's still stuck in a million tonnes of rock.
But it's easy to go too far in the other direction. If you set your criteria to only pick up the brightest objects, and limit your search to the cleanest parts of the data, you can be pretty confident your reliability is close to 100% : everything you've found is almost certainly a real galaxy. Unfortunately brighter galaxies are rarer than fainter ones, so this means your completeness is much lower, potentially missing all the really interesting objects.
How do we get around this ?
Customised catalogues
In short there are no foolproof solutions. We have to tailor our approach to what it is we want. There are times when completeness is the most important, such as when we present a first catalogue from a data set : we want to make sure as many real sources are found as possible to extract the maximum scientific returns. We just need to warn everyone, "look, this might not be entirely reliable yet, do your own follow-up observations if you need to be sure".
But when we need to compare different catalogues, reliability may be what we're after. In this case we need to be sure we're only comparing real sources, so we might have to trim one or more of our samples to ensure we're comparing sources of the same characteristics at the same sensitivity level.
Completeness, and to a lesser extent reliability, can only ever be estimated. You can never know with 100% certainty that you've found every single source present. There are some ways around this though : we can compare the catalogues generated by different observers using different source extraction techniques, and perhaps best of all by having those observers check their methods using large numbers of artificial sources that we implant into the data. A completeness value can't be given with perfect accuracy, but we can still give a meaningful estimate of it.
The situation for reliability is a bit better. In principle you can do follow-up observations for every source. This isn't practical for every single detection but it can often be do-able for every interesting source in a particular catalogue. More problematic here is that since you can't establish completeness very well at lower brightnesses, you can't really do the same level of follow-up for the faintest objects either – your samples will be biased, because you'll be missing some fraction of the faintest objects. Again, you can still give a meaningful, if imperfect, value, however.
Sensitivity
Both completeness and reliability are functions both of the data and the source extraction techniques used. Different search techniques and different data processing methods can reveal quite different sources even in the same data set, which is one reason preserving data is essential : you don't know what techniques will be invented in the future for revealing stuff you never suspected was there. Still, it'd be nice to have a quantitative estimate of sensitivity that's independent of the search methodology.
In fact there is :
- SENSITIVITY is the typical flux level of a single, random resolution element. There's just no way at all you could ever detect anything fainter than this because by definition it would be indistinguishable from noise*.
* There are ways which circumvent this but only to an extent, and with many major caveats – see the stacking pages.
But remember, raw sensitivity and completeness are not necessarily the same thing at all. A source with a peak signal that's even ten times the noise value (signal to noise ratio, sometimes abbreviated to SNR or S/N) might still escape detection if it only appears in a pixel or two, while one which has a S/N of just four might be easily detectable if it spans enough of the pixels in the data. Quantifying exactly how this works, and especially how well we do for the AGES and WAVES survey, is something I'm actively involved in (see also this excellent paper from the ALFALFA survey).
Additionally, while sensitivity can be legitimately defined as this very hard lower limit, in practise it's common to be more conservative. We have absolutely zero chance of detecting a single channel emitting at S/N of 1; by definition this appears indistinguishable from the noise ! But do we have any chance of detecting a single channel at a S/N of 2 ? Of 3 ? What if we allow two or three channels ? This is why we talk of completeness limits, and quite improperly we often misuse and confuse it with the true sensitivity limit. In AGES we generally give our "sensitivity limit" as corresponding to a source of ten channels in width at a S/N level of 4.0, but we do in fact occasionally detect some sources fainter than this – some are a bit wider but lower, others are narrower but higher.
The most important point is that all of these are helpful guides rather than strict quantifications. Not perfect, but far from useless.
Related terms
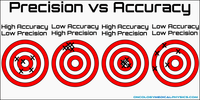
I said accuracy was largely meaningless, but this is only true in media usage. In fact, like completeness and reliability, it has a specific meaning, which is best illustrated by the following graphic :
Accuracy is how close a measurement is to the true value, while precision is about how close repeated measurements of the same source with the same instrument are to each other. These terms both relate to measurements of detected sources, not, despite frequent media misuse, to how good the detection procedure is. A catalogue which is "90% accurate" – and I've seen such descriptions actually used – could very well mean anything. Does it mean they recovered 90% of what was really there (completeness), had 10% misidentifications (reliability), or had measurements which were 90% in agreement with the true value (accuracy) ? Clearly, it's better to keep the meaning as specific as possible.
To be fair, things are a bit better if the search is strictly limited. An algorithm can be meaningfully described as having an accuracy level when it comes to choosing between just two options, if those are the only options it ever receives. If your robot is built for distinguishing cheese from petrol, you're gonna have a hard time if you throw it some flowers – as David Mitchell discovered to his cost.
False positives (a detection of source which turns out to be spurious) and false negatives (failure to detect a real source) are also sometimes used, though not very often in astronomy. I suppose our error rates are just so high that expressing completeness and reliability as percentages has become convention.
A final point is that for all the care we have to take with catalogues, we can completely mitigate this for individual objects. If we think we've detected a galaxy but we're not quite sure, we can observe it as many times as we like with other telescopes. Repeat detections with different instruments constitute the nearest thing we can get to true certainty. Similarly, while we can't rule out that a galaxy might have some undetectable quantity of gas, we can still place stringent upper limits on how much it can have – often more than enough to rule out any particular theoretical model we might be interested in. So while there are a lot of statistical considerations when dealing with the data, it's not quite as bad as it might first appear.
How good are our catalogues, really ?
This is something which is always difficult to estimate ! In my experience, visual extraction is both more effective and more honest. A human can see straight away where a region has been affected by interference (at least the egregious sort), while programming this is not at all easy because the structures are so complex. And humans can find things which are remarkably faint, while their natural reluctance to generate enormous catalogues helps keep their reliability high. Algorithms have no such qualms and will cheerfully spit out catalogues of tens of thousands of pathetic spikes if you set the criteria poorly.
Everyone accepts that visual catalogues are subjective, but it's easy to be fooled into thinking that because an algorithmic approach is objective and repeatable it is therefore better. The problem with this is that objective measurements and objective truths are not the same thing at all. You can easily have an objective, repeatable catalogue which is just a load of nonsense.
This is not to disparage objectivity; it would be far better if we could simply press a button and get a repeatable, high-quality catalogue from a data cube. But at present this is just not the case, with the resulting catalogues needing to be carefully checked by one or more humans – so we may as well accept it and do a visual inspection anyway. Automatic algorithms are still extremely useful as additional checks however, as it's almost inevitable that some sources will be missed, so the more searches of a data set, the better. My suspicion is that the fancy image-identification algorithms than can generate captions for complicated images actually have an advantage in the complexity of the data; for HI we only have brightness to go on and precious little else.
I'm working on quantifying how good our search technique is by injecting large numbers of artificial sources into empty data and searching for them with FRELLED. Spoiler alert : this indeed works well, and we can quantify quite precisely the criteria of the sources we recover and how their parameters affect their detectability. This is something I need to get around to publishing...
Final point : good source extraction needs good logistical management skills. It's an inherently messy business of deciding, "hmm, maybe that's a source, maybe it isn't, what if I check this way", etc. The difficulty is primarily in managing the vast number of resulting tables of definite, unlikely, marginal and definitely spurious sources all found by different methods, and then synthesising them into a harmonious whole that can be safely published. Source extraction is an interesting intellectual exercise but quite different from producing theoretical models or interpreting data.